Proxima actualización XD

Razón en que un segmento es dividido por uno de sus puntos

La razón  "r"es un cosciente que compara que tan grande es una parte del segmento con respecto a la parte
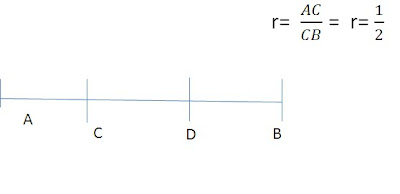
restante, por ejemplo si se divide al segmento AB en tres partes iguales AC, CD Y DB como se muestra en la siguiente figura:

Veamos un ejemplo de esta situación:

Se nos dan los puntos A (1,2) y B (6,8)...

Otro tema muy importante que se deriva de esto y es el como sacar el punto medio de un segmento.

Para esto es muy importante recalcar que la razón del punto medio es a 1.

La formula para localizar las coordenadas en x, y es:

 

Más adelante en otro apartado daremos ejemplos de como aplicar el punto medio... hasta la proxima actua....

CAlCULO DE ANGULO TETA EN COORDENADAS POLARES...

PRIMER CASO:

SEGUNDO CASO:

TERCER CASO:

CUARTO CASO:

PUNTO CARTESIANO A PUNTO POLAR...

Por lo cual lo siguiente es calcular, esto con el teorema de Pitágoras.

                              

Ejemplos de coordenadas polares y distancia de dos puntos..

Bueno, aquí Grillita reportandose... debido a que hubo unos videos como ejemplificación tal vez no quedo claro el procedimiento, así que me tome
la molestia de hacer unas imagenes donde viene de manera muy general lo que se tiene que hacer... XD... YA SI NO SE VUELVE A ENTENDER, REPETIRE LA EXPLICACION PASO A PASO JOJOJOJO... pero avicen...

Primero pondre la de distancia de dos puntos por que fue el ultimo tema, ademas aqui si viene la formula XD...

Ahora el ejemplo de polares.......

 

DISTANCIA ENTRE DOS PUNTOS

Un segmento en el plano cartesiano queda bien definido si conocemos las coordenadas de sus extremos. Si tenemos dos puntos cuales quiera en el plano P(x, y), Q(x2, y2) para saber la longitud del segmento PQ debemos utilizar la sig. Formula:

sistemas de coordenadas polares

Como recordaran en un sistema de coordenadas rectangulares un punto en el plano se representa mediante un par ordenado (x,y).En un sistema de coordenadas polares se selecciona un punto llamado polo, y luego una raya con vértice en el polo, llamado eje polar. Al comparar los sistemas de coordenadas rectangular y polar se observa que el origen y el eje x positivo de las coordenadas rectangulares coinciden con el polo y el eje polar respectivamente,

En un sistema de coordenadas polares, un punto “p” se representa por medio de un par ordenado de números (r, ٥) si r es mayor que ٥, entonces r es la distancia entre el punto y el polo, ٥es un angulo (en grados o radiales) formado por el eje polar y una raya que parte del polo y pasa por el punto. Al par ordenado lo llamamos las coordenadas polares de un punto.

SISTEMA DE COORDENADAS RECTANGULARES.

Bien, esta ocasión veremos lo que serán los sistemas de coordenadas rectangulares que pertenecen al temario de lugares geométricos y sistemas de coordenadas, hasta al final de todos estos temas daremos una seccion de ejemplificacion si asi lo quieren XD...

En este sistema para localizar un punto en el plano utilizaremos como referencia dos rectas perpendiculas:

una horizontal (eje de abscisas) y otra vertical (eje de ordenadas) que se cortan en un punto llamado origen de coordenadas, asociando los ejes con una escala númerica.

De esta formatodo punto en este sistema, queda determinado de forma unica por dos números, estos serán:

 "X" la distancia del origen a la distancia de abscisas, y la distancia de origen sobre el eje de ordenadas "Y";  

 estos dos números los escribimos como la pareja ordenada (X,Y) que son las coordenadas cartesianas de un punto "P".

Estos ejes dividen el plano en 4 regiones llamadas cuadrantes, y los signos de las coordenadas nos demuestra donde se encuentra el punto.